Fig. 1. Sketch del metodo VG. I segmenti continui tra gli eventi definiscono le connessioni “permesse”; quelli tratteggiati definiscono le connessioni “non permesse”
Questa legge di visibilità introduce una differenza tra eventi intensi, che fungono da “hubs” (con un grado di connettività -ossia il numero dei link che vi convergono- maggiore) ed eventi di magnitudo minore come aftershocks, foreshocks, swarms. Se si considera la relazione tra la magnitudo del terremoto M e il numero di connessioni che vi convergono k, si è osserva che la pendenza della relazione M-k è correlata con il b della legge GR (Telesca et al., 2013).
Il lavoro Telesca et al. (Relationship between the Frequency Magnitude Distribution and the Visibility Graph in the Synthetic Seismicity Generated by a Simple Stick-Slip System with Asperities, PloSONE, 9, e106233, 2014) mostra che tale correlazione tra la pendenza M-k e il b della GR non è verificata solo per diverse sequenze sismiche reali, ma anche per sequenze sismiche sintetiche generate da un esperimento di simulazione stick-slip di faglia tettonica (Fig. 2), suggerendo pertanto una sorta di universalità nella relazione tra proprietà sismologiche e proprietà topologiche di sequenze di terremoti (Fig.2)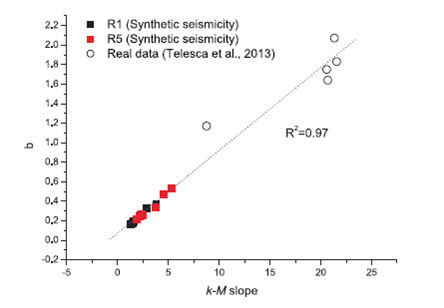
Per informazioni:
Luciano Telesca, CNR-IMAA – luciano.telesca at imaa.cnr.it
Approfondimenti:
Telesca, L., Lovallo, M., Ramirez-Rojas, A., Flores-Marquez, L., Investigating the time dynamics of seismicity by using the visibility graph approach: Application to seismicity of Mexican subduction zone, Physica A 392, 6571–6577, 2013
Telesca, L., Lovallo, M., Ramirez-Rojas, A., Flores-Marquez, L., Relationship between the frequency magnitude distribution and the visibility graph in the synthetic seismicity generated by a simple stick–slip system with asperities, PlosOne, e106233, 2014
Telesca, L., Lovallo, M., Toth, L., Visibility graph analysis of 2002-2011 Pannonian seismicity, Physica A, 416, 219-224, 2014
Telesca, L., Lovallo, M., Aggarwal, S. K., Khan, P. K., Rastogi, B. K., Visibility Graph Analysis of the 2003–2012 Earthquake Sequence in the Kachchh Region of Western India, Pageoph, doi: 10.1007/s00024-015-1034-9